Bewijzen van stellingen door
Volledige Inductie
→ Speciaal !
→ Ongewoon !
Klik op de formule en
het bewijs komt rechts
|  |
| |
|
|
|
Dn xn = n! of (xn)(n) = n!
|  07 07 |
=\frac{x}{1-x}\;&space;\Rightarrow&space;\;\;&space;f^{(n)}(x)=\frac{n\,!}{(1-x)^{n+1}})
|  J3 J3 |
M.Rij met reden q → 
|  09 09 |
|
|
cos (θ + n  ) = (−1)n cos θ ) = (−1)n cos θ
|  N5 N5 |
|
sin (2nx) = 2n.sin x.cos x .cos 2x....cos (2n−1x)
|  16 16 |
|
tan 10n = tan 100 voor n = 2, 3, 4, ...
|  60 60 |
|
A.B = B. A ⇒ A.Bn = Bn. A (matrix)
|  68 68 |
 (deelverzamelingen)
(deelverzamelingen)
|  73 73 |
|
D xn = n.xn−1 (afgeleide)
|  78 78 |
|
(r.cis θ)n = rn. cis nθ (DE MOIVRE) ℂ
|  81 81 |
Dn sin x = sin (x + n. 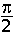 ) )
|  83 83 |
|
Dn (x.ex) = (x + n).ex
|  L4 L4 |
|
Dn (x2.ex) = [ x² + 2nx + n(n − 1) ].ex
|  L4 L4 |

|  89 89 |

|  97 97 |
|
xn − 1 = (x − 1)(xn−1 + xn−2 + ... + 1)
|  T7 T7 |

|  A0 A0 |
)
|  Q9 Q9 |

|   A3 A3 |
|
(1+ sec 2α)(1+ sec 4α)...(1+ sec 2nα ) = tan (2nα).cot α
|  A7 A7 |
=\frac{\sin\:&space;(2^{n+1}\alpha&space;)&space;}{2^{n+1}.\sin&space;\alpha&space;})
|  A8 A8 |
t1 = 1 ∧ tn+1 = 3tn− 1 ⇒ tn =  (3n−1 + 1) (3n−1 + 1)
|  B4 B4 |
|
t1 = 1 ∧ tn = 2.tn−1 + n ⇒ tn = 2n+1 − n − 2
|  D4 D4 |
t_{n\!-\!2}\Rightarrow&space;t_n\geqslant&space;\sqrt{n!})
|   S2 S2 |
|
t0=-1, t1=1, tn= 4, tn−1− 3.tn−2 ⇒ tn = 3n − 2
|  J2 J2 |
Aantal diagonalen n-hoek is  n (n − 3) n (n − 3)
|  D3 D3 |
|
Van rij { t n } is s n = 2n − t n ⇒ t n = ? (formule)
|   F7 F7 |

|  G0 G0 |

|  R8 R8 |

|  R9 R9 |

|  T5 T5 |
|
Voor n >13 bestaan x en y zó dat n = 3x+8y (in ℕ)
|   G5 G5 |
|
1 = som van 3, 4, 5,... verschillende stambreuken
|  G6 G6 |
 (Complexe getallen) (Complexe getallen)
|  G9 G9 |

|  E1 E1 |

|  A1 A1 |

|  B0 B0 |
^{n-2}&space;\quad&space;(FIBONACCI))
|   H9 H9 |
(3 + 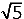 )n + (3 − )n + (3 − 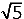 )n is geheel ∀ n ∈ ℕ )n is geheel ∀ n ∈ ℕ
|   I2 I2 |
SPn = 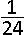 (n − 1).n.(n + 1).(3n+2) (n − 1).n.(n + 1).(3n+2)
|  I7 I7 |
SPOn = 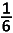 n(n − 1)(3n2 − n − 1) n(n − 1)(3n2 − n − 1)
|  I8 I8 |
tn ≥ (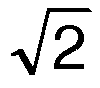 )n−2 ( n = 4,5,...) )n−2 ( n = 4,5,...)
|  J8 J8 |
\sqrt{\cdots&space;}}}\:&space;=\:&space;n+1)
|  K1 K1 |
 (n=1,2, ...) (n=1,2, ...)
|   L1 L1 |
|
a1 = 3 ∧ an = 3 an−1 − 2 ⇒ an = 2.3n−1 + 1
|  L5 L5 |
|
t1 = 3 ∧ tn+1 = 3 tn + 4 ⇒ tn = 5.3n−1 − 2
|  R7 R7 |
|
t0 = 3 ∧ tn+1 = 2 tn + 2n − 4 ⇒ tn = 2n− 2n + 2
|  S3 S3 |
|
\(\small{\displaystyle\sum_{i=1}^{n}\;i.2^{n-i}=2^{n+1}-(n+2)}\)
|  L9 L9 |
|
som hoeken n-hoek is (n − 2).180°
|  N7 N7 |
|
\(\small \# \, V = n \; \Rightarrow \; \mathbb {P}\, (V)=2^{n} \)
|  O0 O0 |
|
\(\frac{3n^2}{2}\!+\!\frac{2n^3}{3}\!-\!\frac{n}{6}\in \mathbb{N}\quad ,\forall n \in \mathbb{N} \)
|  S7 S7 |
|
\(\frac{n^5}{5}+\frac{n^3}{3}+\frac{n^2}{2}-\frac{n}{30}\in \mathbb{N}\quad ,\forall n \in \mathbb{N} \)
|  T8 T8 |
|
\(\frac{n^7}{7}+\frac{n^5}{5}+\frac{2\,n^3}{3}-\frac{n}{105}\: \in \mathbb{N}\; ,\forall n \in \mathbb{N} \)
|  T9 T9 |
V o l l e d i g e
i n d u c t i e
Mathematical induction (Engels)
Vollständige Induktion (Duits)
Induction Mathématique (Frans)
Indução matemática (Portugees)
Induzione matematica (Italiaans)
Inducción completa (Spaans)
www.symptoma.ro
→ telling vanaf 20 maart. 2021 ←

